Bei einer statistischen Analyse sollte man kritisch die Möglichkeit überdenken, wesentliche Merkmale unter Umständen übersehen zu haben. So ist es beispielsweise möglich, dass zwar eine Beeinflussung von einem Merkmal A auf ein Merkmal B stattfindet, aber nicht direkt, sondern über ein direktes Merkmal C. Berücksichtigt man C in der Analyse nicht, kann dies zu falschen Schlüssen und zu Scheinkorrelationen führen.
Was ist eine Scheinkorrelation?
Eine Scheinkorrelation liegt vor, wenn man eine hohe Korrelation zwischen zwei Merkmalen beobachtet, die inhaltlich nicht gerechtfertigt ist. Solche scheinbaren Zusammenhänge können dadurch bewirkt werden, dass ein mit beiden beobachteten Merkmalen hochkorreliertes drittes Merkmal übersehen wird und somit unberücksichtigt bleibt.
Scheinkorrelation an einem Beispiel
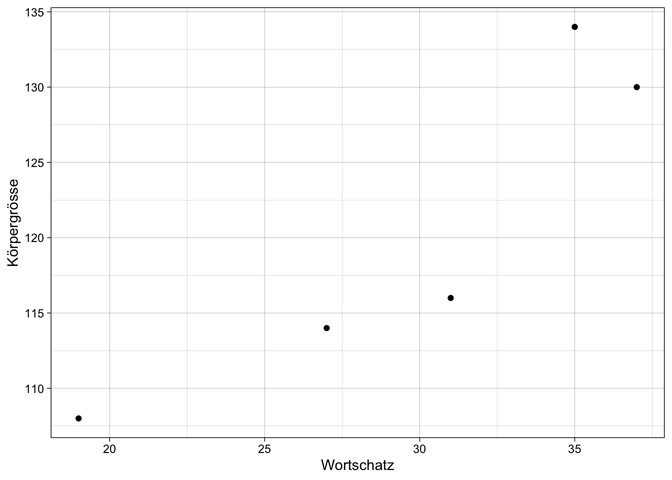
Bei fünf zufällig ausgewählten Kindern wurden der Wortschatz X und die Körpergrösse Y in Zentimeter gemessen. Dabei erfolgte die Messung des Wortschatzes über die Anzahl der verschiedenen Wörter, welche die Kinder in einem Aufsatz über die Aktivitäten in ihren Sommerferien benutzten. Gehen wir davon aus, es liegen die folgenden Daten vor:
| x | y |
|---|---|
| 37 | 130 |
| 31 | 116 |
| 19 | 108 |
| 27 | 114 |
| 35 | 134 |
Werden die Daten in einem Streudiagramm visualisiert, erkennt man einen starken positiven Zusammenhang, d.h. je grösser der Wortschatz ist, desto grösser ist auch das Kind.
Weil beide Merkmale metrisch sind, kann die Stärke des Zusammenhangs mithilfe des Korrelationskoeffizienten nach Bravais-Pearson gemessen werden.
Das Ergebnis von 0.9029815 scheint auf einen starken, linearen, positiven Zusammenhang hinzuweisen.
Sachlogisch lässt sich nicht erklären, weshalb ein Zusammenhang von zunehmender Körpergrösse und Wortschatz vorliegt. Vielmehr scheint hier das Problem zu bestehen, dass eine andere entscheidende Variable diesen Zusammenhang bewirkt. In diesem einfachen Beispiel ist die Lösung des Problems naheliegend. Mit wachsendem Alter nehmen sowohl Körpergrösse als auch Wortschatz zu. Nimmt man das Alter als drittes Merkmal (Variable Z) gemessen in Jahren hinzu, ergeben sich folgende Korrelationskoeffizienten:
| x | y | z |
|---|---|---|
| 37 | 130 | 12 |
| 31 | 116 | 7 |
| 19 | 108 | 6 |
| 27 | 114 | 8 |
| 35 | 134 | 13 |
rXZ = 0.8436008
rYZ = 0.9822333
Ein drittes, mit den anderen beiden Merkmalen hochkorreliertes Merkmal blieb zunächst unberücksichtigt. Der Effekt war die Beobachtung einer Scheinkorrelation zwischen den ersten beiden Variablen.
In diesem Beispiel ist es offensichtlich, dass das Alter der Kinder die eigentlich entscheidende Grösse ist, um die Scheinkorrelation aufzuklären. Oft lässt sich aber für eine beobachtete Korrelation eine Erklärung finden, die zwar nachvollziehbar scheint, aber dennoch die eigentlich entscheidenden Zusammenhänge übersieht.
Ein dafür gerne genutztes Beispiel ist der Zusammenhang zwischen steigendem Glace-Konsum und dem Zunehmen von Sonnenbrand. Beide Merkmale treten im Sommer vermehrt auf, im Winter seltener. Ein logischer Zusammenhang zwischen den beiden Variablen besteht dennoch nicht. Erst wenn als drittes Merkmal die steigenden Temperaturen im Sommer in die Analyse miteinbezogen werden, ist es offensichtlich, wie die Merkmale zusammenhängen.
In umfangreicheren Studien ist ein solches Problem üblicherweise nicht ganz einfach zu lösen, weil zu Beginn der Studie häufig unklar ist, welche Merkmale überhaupt wichtig sind und somit erhoben werden sollen. Wird ein entscheidendes Merkmal in der Studienplanung übersehen, so lässt sich dieses meist nicht mehr nachträglich erheben.